拉格朗日乘数法笔记

在求解函数最优化问题中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）条件是两种最常用的方法。函数有等式约束时使用拉格朗日乘子法，函数有不等约束时使用KKT条件。本文简要的复习下拉格朗日乘数法的浅层次问题。

本文简书链接

拉格朗日乘数法

在求解函数最优化问题中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）条件是两种最常用的方法。函数有等式约束时使用拉格朗日乘子法，函数有不等约束时使用KKT条件。

本篇文章主要整理拉格朗日乘子法

这种方法可以将一个有 n 个变量与 k 个约束条件的最优化问题转换为一个解有 n + k 个变量的方程组的解的问题。这种方法中引入了一个或一组新的未知数，即拉格朗日乘数，又称拉格朗日乘子，或拉氏乘子，它们是在转换后的方程，即约束方程中作为梯度（gradient）的线性组合中各个向量的系数。

总结伸手党，比如两个变量求最优时，求 f(x,y) 在条件 g(x,y)=c 时的最大值，我们可以引入新变量拉格朗日乘数 λ，这时我们只需要下列拉格朗日函数的极值,此时就回归到了无约束时的最值问题：

F(x,y,λ)=f(x,y)+λ⋅(g(x,y)−c)

无约束时函数最优问题

这种问题，通常的解决办法是，对各变量求偏导，使得各偏导同时为零得到驻点。再判断驻点是否为极值点，最后代入原函数验证最优。

等式约束时函数最优问题

设目标函数为 f(x,y)， 约束条件为 g(x,y)=c。问题是如何在满足约束条件的情况下，使得目标函数最大(最小)。

使用一个例子来描述这个问题：在双曲线 xy=3 的情况下，哪个点离原点最近。

f(x,y)=x2+y2g(x,y)=xy=3

如图：

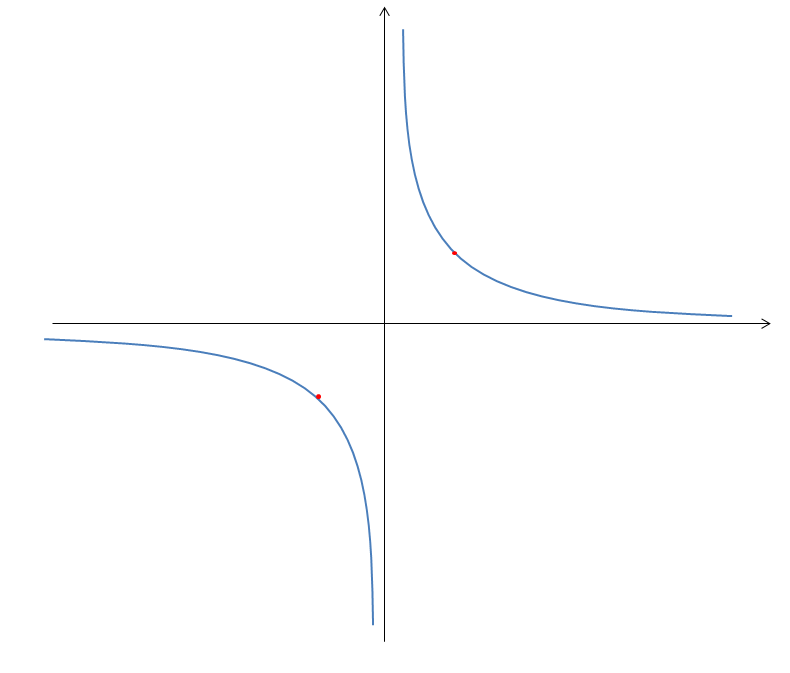
那么f(x,y) 可以被描述为无数个一圈圈的等高线(图中所有颜色的圆圈线)，这些等高线与双曲线相交的点是满足约束条件的点。那么离原点最近的点，就是等高线与双曲线互切处的点，如图中，红色的点。

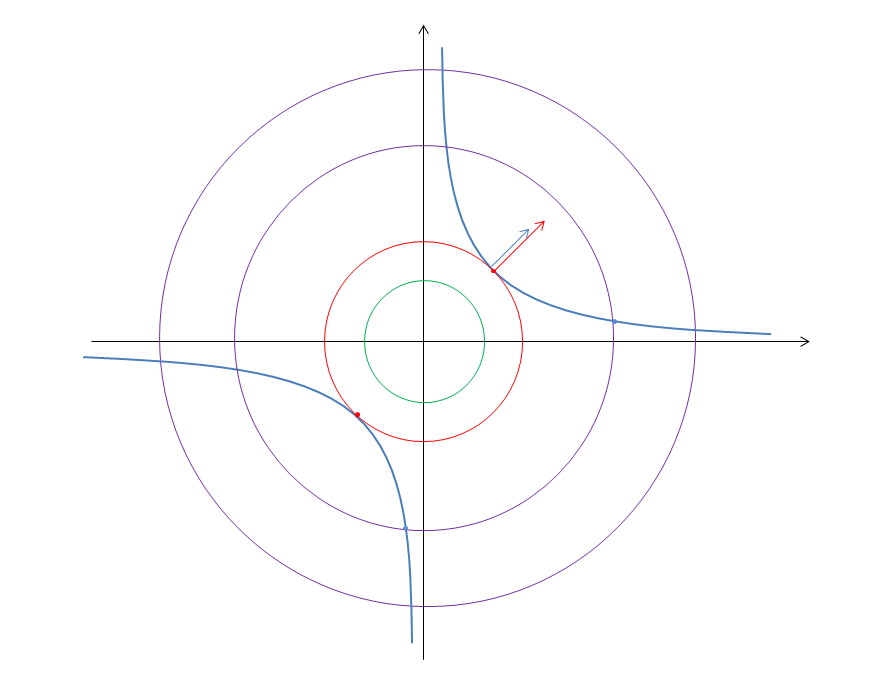
1. 绿色的等高线无法与双曲线相交，没有满足约束条件的解
2. 蓝色点虽然满足约束条件，但并非最优解
3. 只有等高线与双曲线相切的红色的点，才是最优解。

在取最优解时，我们发现只有相切才能取最优解。那么如何判断相切呢？ 那就使用梯度向量（如图中红色蓝色的梯度向量），如果两者梯度向量互相平行时，那么两条曲线相切。于是引入一个参数 λ 使得满足如下梯度公式：

∇f(x,y)=λ⋅∇g(x,y)

那么原目标函数 f(x,y) 和 约束条件 g(x,y) ，在取最优值时满足上述公式那么：

{f′x=λ⋅g′xf′y=λ⋅g′y

此时我们就拥有了三个公式，三个未知数的多项式。把三个未知数全部解出来。代入原目标函数就是函数最值。

最后我们稍微整理下这三条公式:

{f′x−λ⋅g′x=0f′y−λ⋅g′y=0g(x,y)=c

发现原最优问题可以被替换成求F(x,y,λ)=f(x,y)+λ⋅(g(x,y)−c)的最优问题。且这个问题不受g(x,y)所约束，因此可以使用无约束时函数最优问题来解决。至此呼应了开头伸手党结论。